2D to 3D Projection

This tutorial demonstrates how to implement a 2D to 3D projection system using raycasting in SplashKit, combining a first-person 3D view with a top-down 2D map to visualise the player's field of view and interactions in a grid-based environment.
Written by: Shaun Ratcliff
Last updated: 08 Dec 24

Full C# and Python code for this tutorial is still in development.

---

Introduction to 2D to 3D Projection Using Raycasting

Raycasting is a powerful technique in game development that allows us to simulate how rays of light or vision interact with objects in a virtual environment. While it is commonly used for simple collision detection or line-of-sight mechanics, it also serves as the foundation for more advanced applications, such as creating 3D effects in 2D environments. By projecting a 2D map into a first-person 3D perspective, we can simulate a 3D world using only 2D assets—a technique famously used in early 3D games like Doom and Wolfenstein 3D.

In this tutorial, we’ll explore how to use SplashKit to build a 2D to 3D raycasting system. You’ll learn how to:

• Cast rays from a player’s position to detect walls in a grid-based map.
• Use ray distances to render a first-person 3D view of the environment.
• Display a top-down 2D map alongside the 3D view for reference.

This approach is ideal if you are looking to take your games to the next level. Even beginners can experiment with these concepts to add a visually striking effect to simpler applications, such as dungeon crawlers or maze games. By the end of this tutorial, you’ll have a dynamic system that combines 2D and 3D perspectives, bringing your virtual worlds to life.

Checkpoint!

We recommend you first familiarise yourself with the Raycasting Basics tutorial before proceeding with this one. This will provide you with a solid understanding of the fundamental principles of raycasting and how to effectively make use of the SplashKit functions.

Important SplashKit Functions Used in This Tutorial

1. Vector Magnitude
2. Vector From Angle
3. Vector Point To Point
4. Point Offset By

The Basics of 2D to 3D Projection

Imagine transforming a flat blueprint of a maze into an immersive first-person view, where walls rise around you as you move through the space. This is the essence of raycasting in creating 3D projections. The map is represented as a simple grid of numbers, where 1 represents walls, and 0 represents empty spaces.

// Map grid (1 = wall, 0 = empty space)
const std::vector<std::vector<int>> MAP = {
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
    {1, 0, 0, 0, 0, 0, 0, 0, 0, 1},
    {1, 0, 0, 0, 0, 0, 0, 0, 0, 1},
    {1, 0, 0, 1, 1, 0, 1, 0, 0, 1},
    {1, 0, 0, 1, 0, 0, 1, 0, 0, 1},
    {1, 0, 0, 1, 0, 0, 1, 0, 0, 1},
    {1, 0, 0, 1, 0, 1, 1, 0, 0, 1},
    {1, 0, 0, 0, 0, 0, 0, 0, 0, 1},
    {1, 0, 0, 0, 0, 0, 0, 0, 0, 1},
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
};

From the player’s position on this grid, rays are “cast” outward in the direction they are facing, acting like beams of light or vision probing the environment.

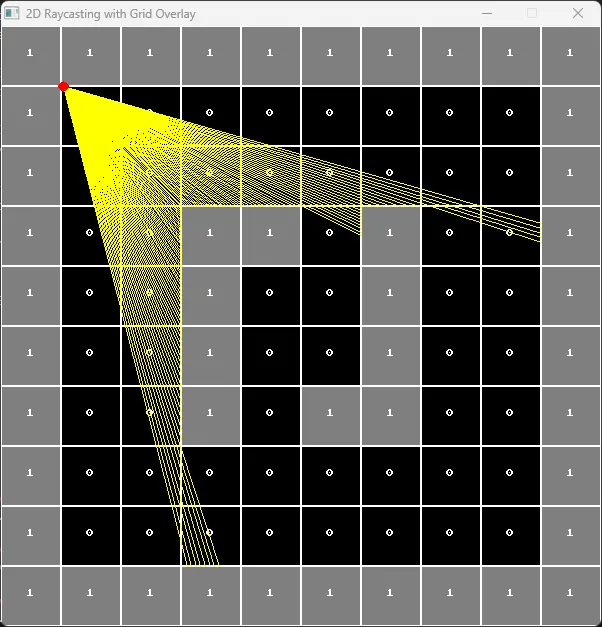
These rays detect the distance to walls in their path. To generate a 3D projection, we can apply the following principles:

1. The closer the wall, the taller it appears on the screen; the farther away, the shorter it looks.
2. By calculating the height of these walls and drawing them as vertical wall slices, we create the illusion of depth.
3. Repeat this process for multiple rays across the player’s field of view to produce a complete first-person perspective. This process transforms the flat 2D map into a visually immersive 3D environment.

Mapping Ray to Screen Projection

In 3D projection, the screen is divided into vertical slices, with each ray corresponding to one slice along the x-axis. The number of rays determines the level of detail in the projection, as each ray extends outward from the player’s position, scanning the environment for walls.

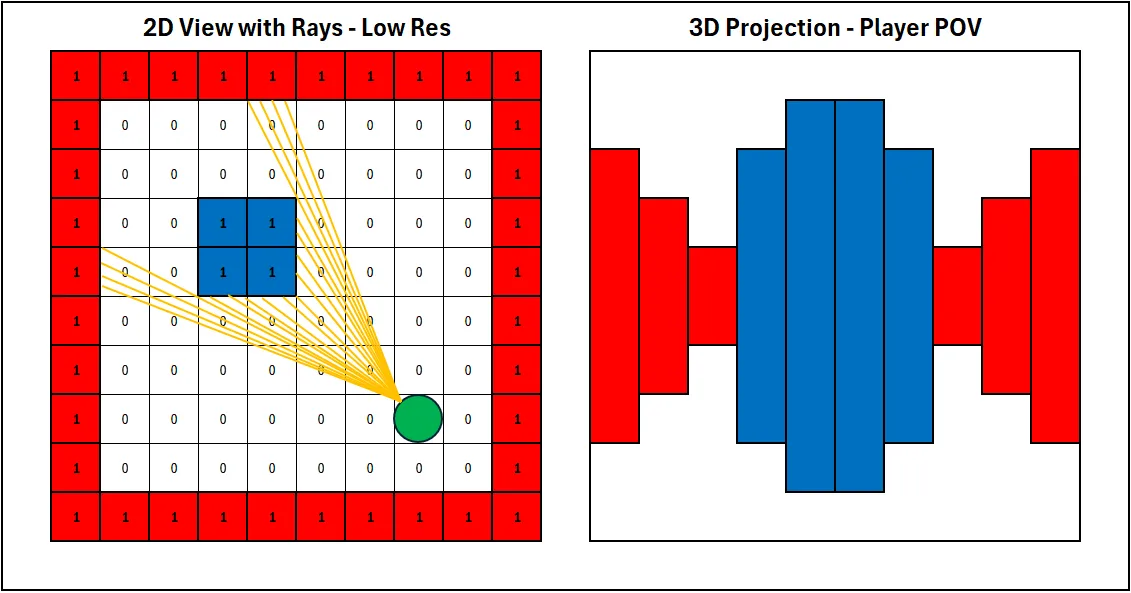
The direction of each ray is calculated based on the player’s position and field of view (FOV). The distance to the nearest wall is then used to render the corresponding slice on the screen. This process creates the illusion of depth and perspective, transforming a flat 2D map into a dynamic, 3D-like experience.

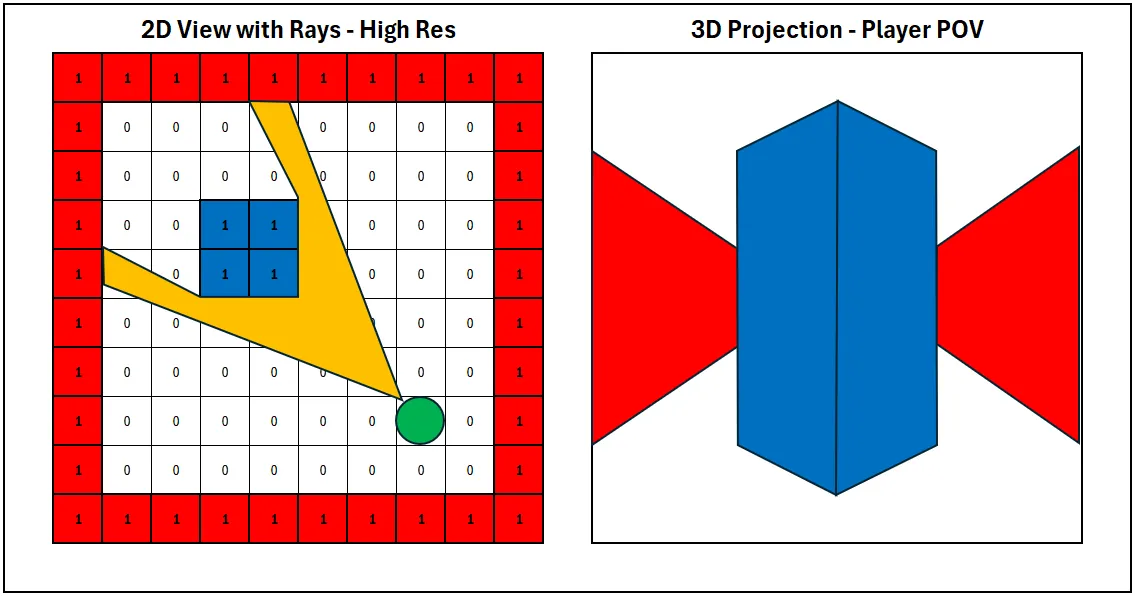
Increasing the number of rays and vertical slices enhances the quality of the projection, resulting in smoother visuals and greater detail, while fewer rays produce a simpler, blockier effect.

Casting a Single Ray

The cast_single_ray function is a continuous loop where:

• The ray moves forward incrementally, checking each position it touches.
• If it hits a wall or exceeds the maximum allowable distance, the function calculates and returns the distance to the wall.

By repeating this process for multiple rays across the field of view, the scene can be projected onto the screen slice by slice.

double cast_single_ray(const Player &player, double ray_angle)
{
    vector_2d ray_dir = vector_from_angle(ray_angle, 1.0);
    point_2d ray_position = player.position;

    while (true)
    {
        ray_position = point_offset_by(ray_position, ray_dir);

        int map_x = static_cast<int>(ray_position.x / TILE_SIZE);
        int map_y = static_cast<int>(ray_position.y / TILE_SIZE);

        vector_2d to_ray = vector_point_to_point(player.position, ray_position);
        double distance = vector_magnitude(to_ray);

        if (!is_within_map(map_x, map_y) || MAP[map_y][map_x] == 1)
        {
            return distance; // Return the distance to the intersection
        }

        // Stop the ray if it exceeds the max distance
        if (distance > MAX_RAY_DISTANCE)
        {
            return MAX_RAY_DISTANCE;
        }
    }
}

Define Ray Direction: The ray’s direction is calculated using a provided ray_angle. This is converted into a unit vector using SplashKit’s vector_from_angle function. This vector determines how the ray “steps” through the virtual environment.

vector_2d ray_dir = vector_from_angle(ray_angle, 1.0);

Advancing the Ray: The ray starts at the player’s current position. This ensures the ray originates from the player’s viewpoint. The ray advances step by step in the direction defined by ray_dir. Each step updates the ray_position by incrementing it using the point_offset_by function.

point_2d ray_position = player.position;
ray_position = point_offset_by(ray_position, ray_dir);

Check Ray Position: The ray’s current position is converted into map grid coordinates (map_x, map_y) to check for collisions with walls (represented as 1 in the map). If the ray hits a wall or moves out of bounds, the function calculates the distance and stops.

int map_x = static_cast<int>(ray_position.x / TILE_SIZE);
int map_y = static_cast<int>(ray_position.y / TILE_SIZE);

if (!is_within_map(map_x, map_y) || MAP[map_y][map_x] == 1)
{
    return distance; // Return the distance to the intersection
}

Calculate Distance: At each step, the distance between the player’s position and the ray’s current position is calculated. If this distance exceeds the maximum ray distance, the ray stops to avoid unnecessary calculations.

vector_2d to_ray = vector_point_to_point(player.position, ray_position);
double distance = vector_magnitude(to_ray);

if (distance > MAX_RAY_DISTANCE)
{
    return MAX_RAY_DISTANCE;
}

Breaking Down the Projection Process

At its core, raycasting reduces the complex task of simulating a 3D environment to drawing a series of lines with mathematical precision. Each ray serves as a “scanner,” collecting data about the environment and translating it into a visually coherent projection.

1. Determine the Ray Angle - Calculate the angle of each ray relative to the player’s FOV. This determines the direction in which the ray will “travel” across the virtual environment.
2. Iterate Across the Screen - Create a loop that corresponds to the width of the screen. Each iteration represents a vertical column of the screen and a specific ray within the FOV.
3. Calculate Wall Height - Use the inverse of the distance to determine the wall’s height on the screen. Divide a constant (e.g., half the screen height) by the distance to achieve this.
4. Draw the World - Render a line for the ceiling (top of the screen to the top of the wall height), for the wall (corresponding to the calculated wall height), and the floor (bottom of the wall to the bottom of the screen) to draw the world.
5. Repeat for All Rays - Repeat this process for every ray, effectively rendering each column of the screen. The result is a projection that simulates depth and perspective in the environment.

Projecting Your 3D World

Determine the Ray Angle

The first step in our raycasting process is to calculate the angle of each ray relative to the player’s FOV. Each ray will “travel” outward from the player’s position, probing the environment for walls. The angle of each ray determines its direction, ensuring that rays span the entire FOV evenly.

Each ray represents a specific vertical slice of the screen, and its angle is calculated relative to the player’s current viewing direction. This is achieved by dividing the FOV into equal increments, with one ray per vertical slice.

Tip

Match the number of rays to the screen width for a 1:1 mapping (e.g., 600 rays for a 600-pixel wide screen). This ensures a smooth and visually accurate projection without unnecessary overhead. You can add a scaling factor to this if you want to adjust for performance.

1. Start with the Player’s FOV: Define the total field of view (e.g., 60 degrees) and determine how many rays will be cast.
2. Divide the FOV: Calculate the angular step between rays by dividing the FOV by the total number of rays. This ensures equal spacing.
3. Iterate Through Rays: Begin at the left edge of the FOV and incrementally step through each ray until the rightmost edge is reached. Each ray’s angle will determine its direction in the virtual environment.

Note

You will need to ensure that you start casting your rays from either side of the player’s current viewing angle. By halving the player FOV and then casting rays from that value subtracted from the current player angle, you will get a true FOV.

const double PLAYER_FOV = 60.0;                       // Player FOV in degrees
const int NUM_RAYS = 600;                             // Total number of rays to be cast

double ray_angle = player.angle - (PLAYER_FOV / 2.0); // Start from the leftmost edge of the FOV
double angle_step = PLAYER_FOV / NUM_RAYS;            // Calculate the angular step for each ray

Iterate Across the Screen

To create the 3D projection, the screen is divided into vertical slices, with each slice corresponding to a ray cast from the player’s position. A loop iterates over the total number of rays, calculating the data for each slice.

For each ray, calculate the distance to the nearest wall:

std::vector<double> distances; // Stores distances for each ray

for (int i = 0; i < NUM_RAYS; ++i)
{
    distances.push_back(cast_single_ray(player, ray_angle));
    ray_angle += angle_step;
}

This loop ensures that every ray spans the FOV, producing a smooth visual projection.

Calculate Wall Height

The wall height is then calculated based on the distance of each ray to its nearest intersection with a wall. This calculation is essential to creating the illusion of depth, as closer walls appear taller while distant walls appear shorter.

Maths

Rays cast at angles other than directly forward experience perspective distortion (or a “fish eye” effect). This is corrected by scaling the distance using the cosine of the ray’s angle relative to the player’s view direction:

double corrected_distance = distances[i] * cos(degree_to_radians(i * (PLAYER_FOV / NUM_RAYS) - (PLAYER_FOV / 2.0)));

This correction ensures that walls maintain consistent proportions, regardless of their angle within the player’s field of view (FOV).

The height of the wall on the screen is inversely proportional to the corrected distance. This means that closer walls occupy more vertical screen space, while farther walls take up less:

int wall_height = static_cast<int>((TILE_SIZE / corrected_distance) * SCREEN_HEIGHT);

Using the calculated wall height, the top and bottom positions of the wall slice are computed to center the wall vertically on the screen:

int wall_top = (SCREEN_HEIGHT / 2) - (wall_height / 2);
int wall_bottom = (SCREEN_HEIGHT / 2) + (wall_height / 2);

These boundaries ensure that walls are drawn in the correct location relative to the player’s viewpoint.

Draw the World

The final step combines rendering the ceiling, walls, and floor to create a complete first-person perspective. Each vertical slice of the screen is divided into three distinct sections: the ceiling, the wall, and the floor. Together, these elements form a cohesive, immersive view of the world.

Draw the Ceiling

The space above the wall height represents the ceiling. A line is drawn from the top of the screen (0) to the top of the wall slice (wall_top), filling this area with a ceiling colour. This ensures the upper portion of the screen reflects the absence of walls in that vertical slice.

Draw the Wall

The wall slice is the focal point of the projection. A vertical line is drawn between wall_top and wall_bottom to represent the wall section corresponding to the ray’s intersection point. The height of this line is determined by the wall height calculated in the previous step, and its brightness is adjusted based on the wall’s distance to achieve more depth.

Draw the Floor

The floor occupies the space beneath the wall slice. A line is drawn from wall_bottom to the bottom of the screen (SCREEN_HEIGHT), filling the remainder of the screen with a floor colour. Like the ceiling, the floor provides spatial context and completes the projection.

Note

In this code, the ceiling and floor are represented by blank space, but you could explicitly draw lines to fill these areas. Alternatively, you could fill these areas with an image (or a series of images) to provide the illusion of a sky or a floor.

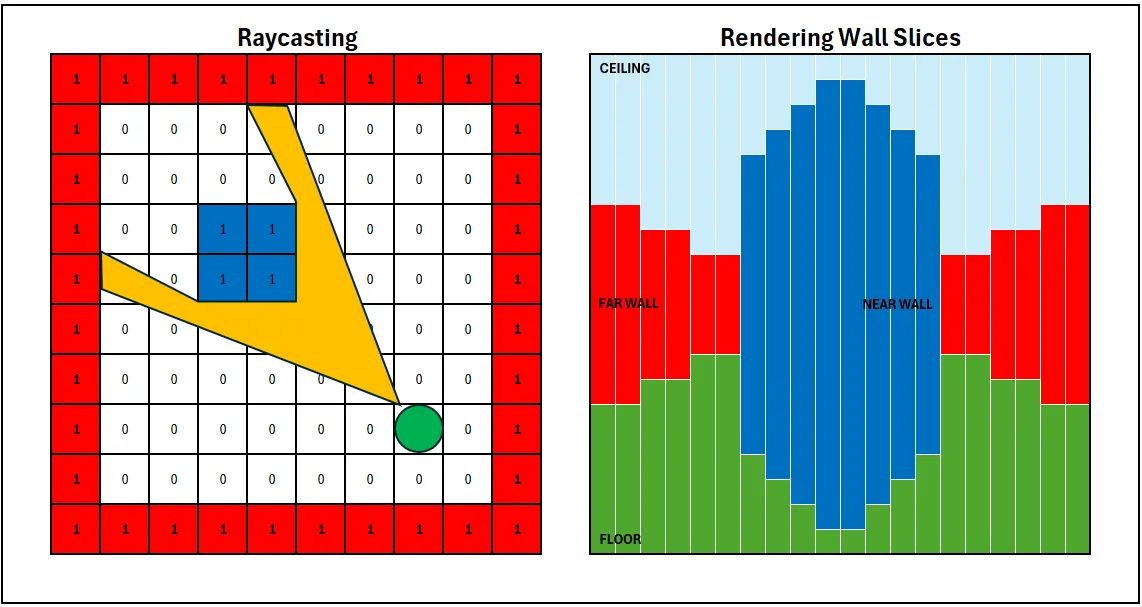
Repeat for All Rays

To create the full 3D projection, the process described in the earlier steps—calculating the ray angle, casting rays, determining wall distances, calculating wall heights, and drawing ceiling, wall, and floor slices—is repeated for every ray in the player’s field of view. Each ray corresponds to a single vertical column on the screen, and by rendering all rays sequentially, the scene is constructed line by line.

// Draw wall slices for each ray
for (int j = 0; j < ray_width; ++j)
{
    int screen_x = i * ray_width + j;
    if (screen_x < SCREEN_WIDTH)
    {
        draw_line(wall_color, screen_x, wall_top, screen_x, wall_bottom);
    }
}

Putting it All Together

Now that you have an understanding of how it all works, let’s see it all in action. Click the Test Code in SplashKit Online button below to load the SplashKit Online IDE and run the code yourself. You can load the 2D version, the 3D version, or the side-by-side 2D + 3D version to explore how they function in real-time.

• The 2D version shows the player navigating a grid-based map from a top-down perspective. Rays are cast outward from the player to detect walls, visualised as yellow lines. This view is ideal for understanding how raycasting works conceptually.

• The 3D version translates the 2D grid into an immersive first-person view, where walls are rendered as vertical slices based on the player’s field of view and the distance to the nearest wall. The perspective dynamically adjusts as the player moves and rotates.

• The combined 2D + 3D version displays both views side by side. The left half of the screen shows the 3D first-person projection, while the right half provides the 2D top-down perspective with rays. This setup helps you connect the 2D calculations to their 3D representation.

Try modifying the map, field of view, or the number of rays cast to see how these parameters affect the visuals. This is a great way to deepen your understanding of raycasting and its practical applications!

2D

Test 2D Code in SplashKit Online

3D

Test 3D Code in SplashKit Online

2D + 3D

Test 2D + 3D Code in SplashKit Online

Conclusion

You’ve now seen how raycasting works to create both a 2D map and a 3D projection of a grid-based environment. By combining mathematical calculations with simple rendering techniques, you can create an interactive program that connects these perspectives in real time. From here, you can experiment with the code by modifying parameters like field of view, map layouts, or even introducing interactive elements. These changes will help you explore the potential of raycasting for your own projects.